Discontinuous Galerkin Finite Element Solver

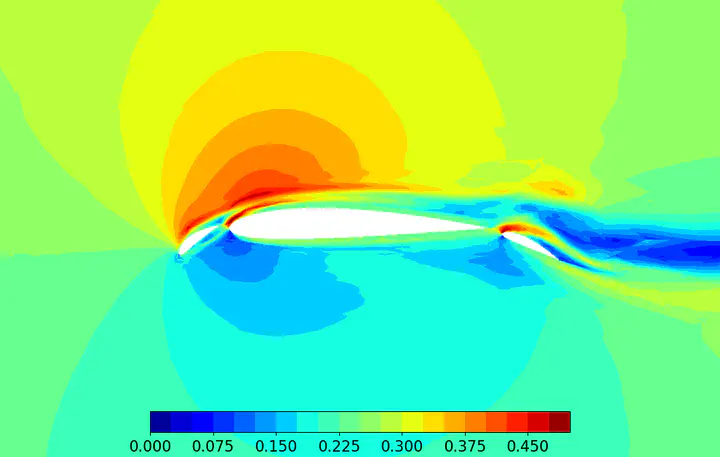
The project involved creating a discontinuous Galerkin (DG) finite element solver tailored for predicting the flow field around a 2D three-element airfoil. The DG solver employed full-order Lagrange basis functions on each triangular element and utilized an explicit fourth-order Runge-Kutta (RK4) time-stepping method to advance the solution to steady-state. It accommodated cases up to (p=3) with (p) representing the order of approximation, utilizing quadrature for integration.

In the DG method, states were treated as functions within a cell. To ensure accurate and physically meaningful solutions, the airfoil elements were curved to align with the true geometry, allowing precise calculation of surface states even on coarse meshes. The implementation included curved boundary edges, and the DG solver was adapted to consider varying transformations from reference to global coordinates for curved elements.

For validation, the team conducted freestream tests and freestream preservation tests on a coarse grid, ensuring that the residual evaluation function consistently produced machine-precision zero values for a single residual calculation and maintained zero as the solution progressed in time. A subsequent convergence study explored the impact of mesh size and approximation order on the accuracy of lift and drag coefficients for the airfoil.

Additionally, an adaptive algorithm was developed to heuristically identify regions for local refinement based on the Mach number discrepancy between neighboring cells. Results from adaptive runs, including lift, drag, and pressure coefficients, were reported and compared with results obtained on the coarse grid. The steady-state results for (p=0) through (p=3) with wall boundary conditions were then presented, excluding (p=3) due to a stability issue, the reasons for which were discussed. Finally, a convergence study investigated the change in predictions with a larger grid size by observing variations in lift and drag coefficients.