Field Inversion and Machine Learning

When conducting fluid simulations, enhancing solution accuracy often involves employing higher-order solution methods. In the context of finite-volume methods, this typically implies the utilization of spatially second-order accurate techniques. However, maintaining stability in the presence of shocks or other flow phenomena requires careful consideration to ensure total variation diminishment (TVD). For second-order finite volume, common approaches involve the use of gradient limiters like Barth-Jespersen or maximum principle region with projection. Yet, these techniques may introduce excessive diffusion, significantly reducing simulation accuracy (as seen in Barth-Jespersen) or prove challenging and resource-intensive to implement, as in the case of maximum principle region with projection.

Despite its simplified nature, the compressible Euler equations offer valuable insights into the behavior of nearly inviscid or high Reynolds number flows, all with remarkably quick simulation times compared to more detailed methods like Reynolds-averaged Navier Stokes or large eddy simulations. Consequently, there is a demand for computational techniques that maximize the accuracy of solving these equations while minimizing computational costs.

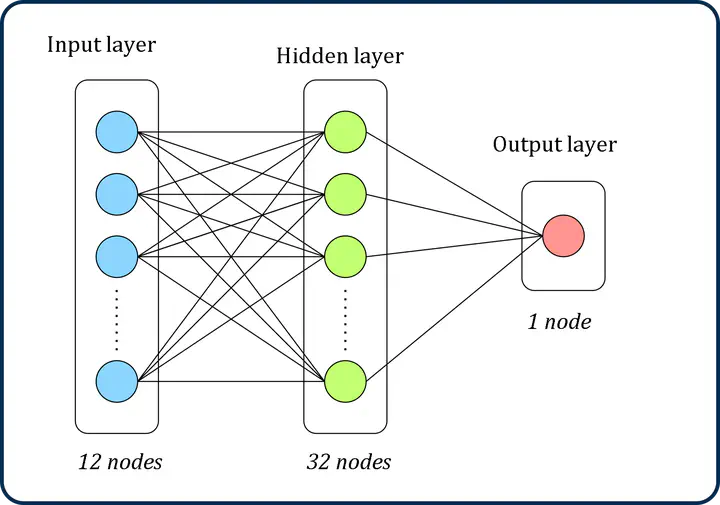
This study introduces a flux limiter field model implemented in a second-order finite volume solver for the compressible Euler equations using field inversion and machine learning (FIML). The integrated flux limiter model adopts a deep neural network (NN). Training data for the NN is acquired through field inversion (FI), determining an optimal flux limiter field for the training cases. Gradient descent is employed to find the optimal field, with the method of adjoints used to calculate the necessary sensitivities. This involves developing code to solve the adjoint system within the solver.