Entropically damped artificial compressibility solver using higher order finite difference schemes on curvilinear and deforming meshes

Abstract

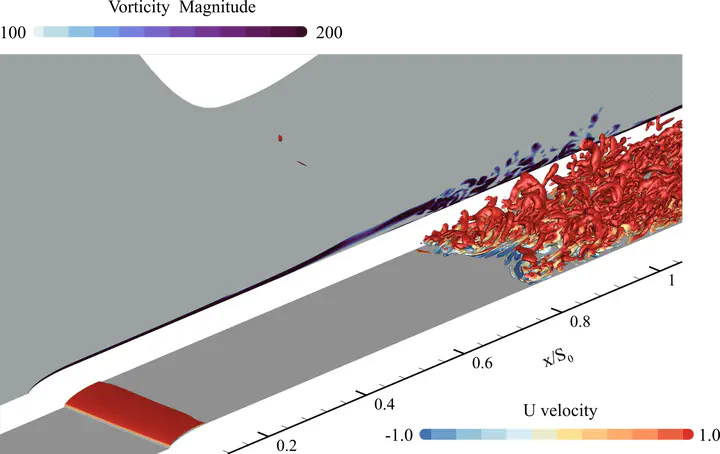
Introduce a groundbreaking Incompressible Navier-Stokes solver harnessing the Entropically Damped Artificial Compressibility (EDAC) methodology. This rendition refines the original EDAC approach, adapting it for generalized curvilinear coordinates to adeptly accommodate intricate geometrical configurations. Addressing intricate computational challenges, our solver demonstrates exceptional efficacy in managing distorted and dynamically deforming meshes, employing advanced high-order finite difference schemes. Rigorous validation across diverse scenarios, encompassing steady and unsteady benchmarks such as Taylor Green Vortex, doubly periodic shear layers, and Inviscid convecting vortex, highlights the solver’s competence across a spectrum of Reynolds numbers. The high-order EDAC method exhibits noteworthy superiority in accuracy compared to its low-order counterparts, even in the face of challenging mesh complexities. Integration of a conservative form of metrics tailored for dynamically deforming meshes yields substantial mitigation of metric cancellation errors. The inherent hyperbolic-parabolic characteristics of the governing equations confer exceptional speed and scalability upon the high-order EDAC solver in curvilinear coordinates, surpassing the performance of elliptic methods. Remarkably, this solver stands as a paragon of efficiency, accuracy, and scalability for fluid dynamics simulations, presenting a robust solution for academic and research endeavors.

Achu Shankar

My research interests include Machine learning, numerical modelling and high performance computing. Solving problems one byte-sized solution at a time.